Diagramas Matriciales: Tu Guía Visual Explicada
Los diagramas matriciales son una herramienta visual eficaz para representar relaciones complejas entre diferentes elementos o variables. Estos diagramas se componen de matrices que cruzan diferentes categorías o variables, permitiendo una visualización clara y sencilla de patrones y tendencias. En este artículo, exploraremos un ejemplo práctico de diagrama matricial, analizando su construcción y aplicación en diferentes campos, como la estadística, la investigación de mercado y la toma de decisiones. Veremos cómo este tipo de diagrama puede ayudar aidentificar relaciones ocultas yrear una mayor comprensión de los datos.
¿Cómo explicar un diagrama matricial?

Un diagrama matricial es una herramienta visual utilizada para organizar y analizar datos de manera estructurada. Esta matriz permite identificar relaciones entre diferentes elementos o categorías, facilitando la toma de decisiones y la planificación estratégica. Para explicar un diagrama matricial, primero se debe comprender su estructura básica, que consiste en filas y columnas que intersectan para formar celdas. Cada celda puede contener información específica que refleja la relación entre los elementos de la fila y la columna correspondiente. El proceso de explicación de un diagrama matricial puede desglosarse en los siguientes pasos: 1. Identificación de Ejes: Comience por identificar los ejes del diagrama. El eje horizontal suele representar una categoría o variable, mientras que el eje vertical representa otra categoría o variable diferente. 2. Llenado de Celdas: Explique cómo se llenan las celdas del diagrama. Cada celda debe contener información relevante que indique la relación o interacción entre los elementos de la fila y la columna correspondientes. Esto puede ser numérico, simbólico o textual. 3. Análisis de Relaciones: Detalle cómo se analizan las relaciones dentro del diagrama. Esto puede implicar la identificación de patrones, la comparación de valores o la evaluación de la intensidad de las relaciones. 4. Interpretación de Resultados: Explique cómo se interpretan los resultados del diagrama. Esto puede incluir la identificación de áreas de oportunidad, la detección de problemas o la formulación de estrategias basadas en los datos presentados. 5. Comunicación Eficaz: Finalmente, subraye la importancia de la comunicación eficaz del diagrama. Esto implica presentar el diagrama de manera clara y comprensible, utilizando colores, leyendas y anotaciones para facilitar su entendimiento.
¿Cómo Identificar los Ejes de un Diagrama Matricial?
Para identificar los ejes de un diagrama matricial, es crucial entender el propósito del análisis. Los ejes representan las categorías o variables que se desean comparar o relacionar.
- Determine el objetivo del análisis y las categorías relevantes.
- Asigne una categoría al eje horizontal y otra al eje vertical.
- Asegúrese de que las categorías sean claras y estén bien definidas para evitar confusiones.
¿Cómo Llenar las Celdas de un Diagrama Matricial?
El llenado de las celdas en un diagrama matricial es fundamental para representar las relaciones entre los elementos de las filas y columnas.
- Recopile los datos necesarios para cada intersección de fila y columna.
- Ingrese la información en las celdas, asegurándose de que sea precisa y relevante.
- Utilice símbolos, números o texto según sea apropiado para representar la relación.
¿Cómo Analizar las Relaciones en un Diagrama Matricial?
El análisis de las relaciones en un diagrama matricial permite extraer conclusiones significativas de los datos presentados.
- Observe las celdas para identificar patrones o tendencias en las relaciones.
- Compare los valores entre diferentes celdas para evaluar la intensidad de las relaciones.
- Utilice herramientas adicionales como gráficos o tablas para complementar el análisis.
¿Qué diagrama se emplea para el análisis de la estructura matricial?
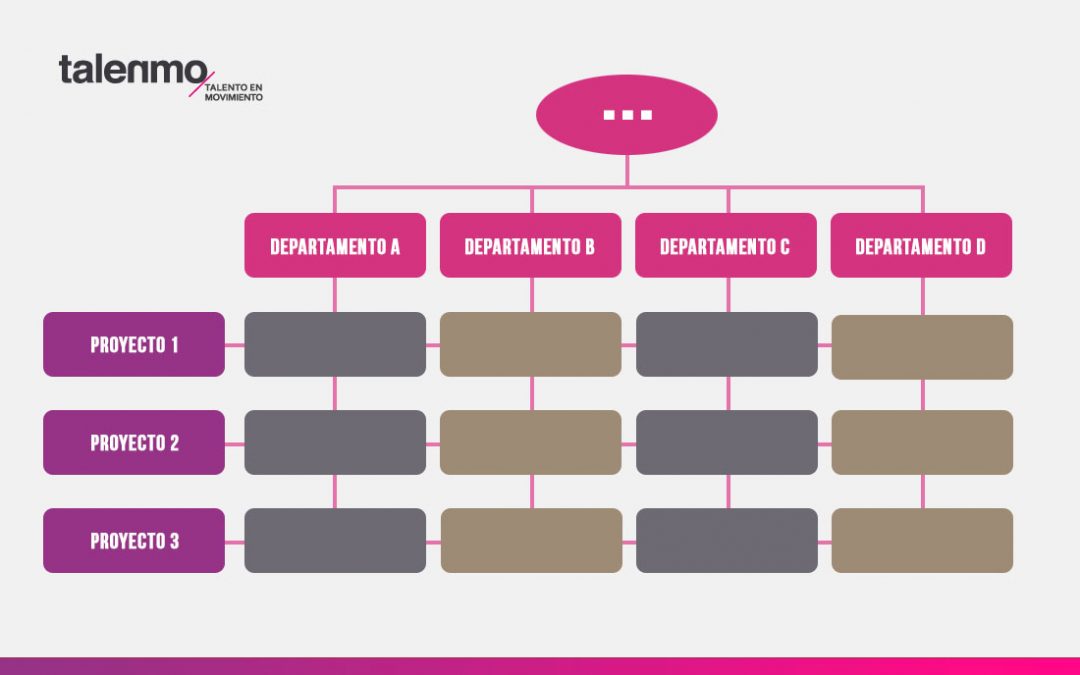
Para el análisis de la estructura matricial, se emplea el Diagrama de Matriz. Este tipo de diagrama es una herramienta visual que permite organizar y relacionar información en una matriz bidimensional, facilitando la identificación de patrones, relaciones y estructuras dentro de un conjunto de datos. Es especialmente útil en la gestión de proyectos, análisis de sistemas y en la toma de decisiones, ya que permite visualizar de manera clara y estructurada las interacciones entre diferentes elementos o variables.
¿Cómo se construye un Diagrama de Matriz?
Para construir un Diagrama de Matriz, se deben seguir los siguientes pasos:
- Identificar los elementos: Determinar los elementos o variables que se van a analizar y que se colocarán en los ejes de la matriz.
- Definir la escala: Establecer la escala o los criterios que se usarán para evaluar las relaciones entre los elementos.
- Llenar la matriz: Completar la matriz con los datos correspondientes, asegurándose de que cada intersección refleje la relación entre los elementos de los ejes.
¿Cuáles son los beneficios de usar un Diagrama de Matriz?
El uso de un Diagrama de Matriz ofrece varios beneficios, entre los cuales se encuentran:
- Claridad visual: Facilita la comprensión de las relaciones complejas entre diferentes elementos de una manera visualmente clara.
- Mejora en la toma de decisiones: Ayuda a los decisores a identificar patrones y tendencias que pueden influir en sus decisiones.
- Optimización de procesos: Permite identificar áreas de mejora y optimizar procesos al visualizar las interacciones y dependencias entre diferentes componentes.
¿En qué contextos se aplica el Diagrama de Matriz?
El Diagrama de Matriz se puede aplicar en diversos contextos, incluyendo:
- Gestión de proyectos: Para visualizar las relaciones entre tareas, recursos y tiempo, facilitando la planificación y el seguimiento.
- Análisis de sistemas: Para entender las interacciones entre diferentes componentes de un sistema y cómo estos afectan su funcionamiento.
- Evaluación de desempeño: Para evaluar el desempeño de diferentes unidades o individuos basándose en múltiples criterios y sus interrelaciones.
Diagrama Matricial: Un Ejemplo Práctico
Un diagrama matricial es una herramienta visual utilizada para representar la relación entre diferentes variables o categorías. A continuación, se presentará un ejemplo práctico de cómo se puede utilizar un diagrama matricial para analizar la relación entre diferentes características de un conjunto de datos.
Definición del Problema
Supongamos que queremos analizar la relación entre la edad, el género y el nivel de educación de un conjunto de personas. Queremos determinar si hay alguna relación entre estas variables y cómo se distribuyen en función de cada una de ellas.
Creación del Diagrama Matricial
Para crear el diagrama matricial, necesitamos definir las variables que queremos analizar y establecer las categorías para cada una de ellas. En este caso, las variables son la edad, el género y el nivel de educación. Las categorías para cada variable serían: Edad: 18-25, 26-35, 36-45, 46-55, 56 o más Género: Masculino, Femenino Nivel de educación: Primaria, Secundaria, Universitaria, Posgrado A continuación, se crea una matriz con las variables en los ejes x e y, y se rellena con los datos correspondientes.
Lectura del Diagrama Matricial
Una vez que se ha creado el diagrama matricial, podemos analizar las relaciones entre las variables. Por ejemplo, podemos ver que: La mayoría de las personas entre 18-25 años son hombres con un nivel de educación secundaria. La mayoría de las personas entre 36-45 años son mujeres con un nivel de educación universitaria. La mayoría de las personas con un nivel de educación posgrado son hombres entre 46-55 años.
Análisis de los Resultados
El diagrama matricial nos permite identificar patrones y relaciones entre las variables que no serían fácilmente visibles mediante otras técnicas de análisis. En este caso, podemos concluir que hay una relación entre la edad y el género en función del nivel de educación.
Ventajas del Diagrama Matricial
El diagrama matricial es una herramienta muy útil para analizar la relación entre múltiples variables. Algunas de sus ventajas son: Permite visualizar la relación entre variables de manera clara y concisa. Facilita la identificación de patrones y tendencias en los datos. Es una herramienta versátil que se puede aplicar a una amplia variedad de conjuntos de datos.
| Edad | Género | Nivel de educación |
|---|---|---|
| 18-25 | Masculino | Secundaria |
| 26-35 | Femenino | Universitaria |
| 36-45 | Masculino | Universitaria |
| 46-55 | Femenino | Posgrado |
| 56 o más | Masculino | Primaria |
Este diagrama matricial es solo un ejemplo, pero ilustra cómo se puede utilizar esta herramienta para analizar la relación entre múltiples variables.
¿Qué es un diagrama matricial?
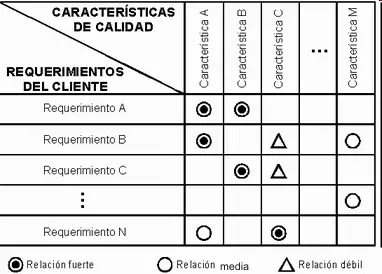
Un diagrama matricial es una representación gráfica que utiliza una matriz para mostrar la relación entre diferentes elementos o variables. Esta herramienta se utiliza comúnmente en diversas áreas, como la ingeniería, la economía, la estadística y la ciencia de la computación, para analizar y visualizar la interconexión entre variables o componentes.
Características de un diagrama matricial
Un diagrama matricial se caracteriza por presentar una serie de características que lo hacen útil para el análisis de sistemas complejos. A continuación, se presentan algunas de las características más importantes:
- Representación gráfica: los diagramas matriciales se presentan en forma de matriz, lo que facilita la visualización de la relación entre las variables.
- Análisis de relaciones: estos diagramas permiten analizar la relación entre diferentes variables o componentes, lo que puede ayudar a identificar patrones y tendencias.
- Flexibilidad: los diagramas matriciales pueden ser utilizados para representar sistemas complejos con un gran número de variables o componentes.
Tipo de diagramas matriciales
Existen diferentes tipos de diagramas matriciales, cada uno con sus propias características y aplicaciones. A continuación, se presentan algunos de los más comunes:
- Diagrama de adjacency: representa la relación entre nodos o vértices en un grafo.
- Diagrama de incidencia: muestra la relación entre nodos y aristas en un grafo.
- Diagrama de asociación: représenta la relación entre variables o características en un conjunto de datos.
Aplicaciones de los diagramas matriciales
Los diagramas matriciales tienen una amplia gama de aplicaciones en diversas áreas, incluyendo:
- Análisis de redes sociales: se utilizan para representar la relación entre individuos o grupos en una red social.
- Ingeniería de sistemas: se utilizan para analizar y diseñar sistemas complejos.
- Minería de datos: se utilizan para identificar patrones y tendencias en grandes conjuntos de datos.
¿Cómo hacer un diagrama de matriz?

Un diagrama de matriz es una herramienta visual que se utiliza para presentar y analizar datos que tienen varias variables o categorías. Esta herramienta es muy útil para identificar patrones, relaciones y tendencias en los datos. A continuación, se presentan los pasos para crear un diagrama de matriz:
Para crear un diagrama de matriz, es necesario seguir los siguientes pasos:
1. Definir el propósito del diagrama: Antes de comenzar a crear el diagrama, es importante definir qué se quiere analizar o presentar. Esto ayudará a determinar las variables o categorías que se deben incluir en el diagrama.
2. Recopilar los datos: Es necesario recopilar los datos que se van a analizar o presentar en el diagrama. Estos datos deben ser precisos y relevantes para el propósito del diagrama.
3. Identificar las variables o categorías: Se deben identificar las variables o categorías que se van a incluir en el diagrama. Estas variables o categorías deben ser relevantes para el propósito del diagrama y deben tener una relación lógica entre sí.
4. Crear la matriz: Una vez identificadas las variables o categorías, se debe crear la matriz. La matriz debe tener tantas filas como variables o categorías se estén analizando, y tantas columnas como datos se tengan para cada variable o categoría.
5. Agregar los datos: Se deben agregar los datos a la matriz, asegurándose de que cada celda contenga la información correspondiente a cada variable o categoría.
Tipos de diagramas de matriz
Los diagramas de matriz se pueden clasificar en diferentes tipos según su propósito y estructura. A continuación, se presentan algunos de los tipos más comunes de diagramas de matriz:
- Diagrama de matriz de correlación: Este tipo de diagrama se utiliza para analizar la relación entre dos o más variables.
- Diagrama de matriz de decisión: Este tipo de diagrama se utiliza para evaluar diferentes opciones o cursos de acción.
- Diagrama de matriz de análisis de causa y efecto: Este tipo de diagrama se utiliza para analizar las causas y efectos de un problema o situación.
Ventajas del diagrama de matriz
Los diagramas de matriz tienen varias ventajas que los hacen útiles para el análisis y presentación de datos. A continuación, se presentan algunas de las ventajas más importantes:
- Facilita la visualización de datos: Los diagramas de matriz permiten visualizar grandes cantidades de datos de manera clara y concisa.
- Ayuda a identificar patrones y tendencias: Los diagramas de matriz permiten identificar patrones y tendencias en los datos que de otra manera podrían pasar desapercibidos.
- Fomenta la toma de decisiones informadas: Los diagramas de matriz permiten evaluar diferentes opciones y tomar decisiones informadas.
Herramientas para crear diagramas de matriz
Existen varias herramientas que se pueden utilizar para crear diagramas de matriz. A continuación, se presentan algunas de las herramientas más populares:
- Microsoft Excel: Excel es una de las herramientas más populares para crear diagramas de matriz. Permite crear matrices y agregar datos de manera sencilla y fácil.
- Tableau: Tableau es una herramienta de visualización de datos que permite crear diagramas de matriz de manera interactiva y dinámica.
- Lucidchart: Lucidchart es una herramienta en línea que permite crear diagramas de matriz y otros tipos de diagramas de manera sencilla y fácil.
¿Qué es un cuadro matricial?
Un cuadro matricial es una representación gráfica utilizada para mostrar la relación entre diferentes elementos o variables de un sistema. Se utiliza para organizar y analizar grandes cantidades de datos, facilitando la toma de decisiones y la comprensión de la información.
Características de un cuadro matricial
Un cuadro matricial se caracteriza por tener una estructura rectangular, con filas y columnas que se cruzan para formar celdas. Cada celda contiene información relacionada con la fila y la columna en la que se encuentra. Los cuadros matriciales pueden ser utilizados para representar información cuantitativa o cualitativa, y pueden ser utilizados en una variedad de contextos, desde la ciencia y la ingeniería hasta la economía y la gestión.
- Los cuadros matriciales permiten la visualización de grandes cantidades de datos de manera clara y concisa.
- Pueden ser utilizados para analizar y comparar diferentes variables y sus relationships.
- Las celdas del cuadro matricial pueden contener información adicional, como gráficos o imágenes, para enriquecer la información.
Tipo de cuadros matriciales
Existen diferentes tipos de cuadros matriciales, cada uno con su propio propósito y características. Algunos de los tipos más comunes son:
- Cuadro de doble entrada: se utiliza para representar la relación entre dos variables.
- Cuadro de triple entrada: se utiliza para representar la relación entre tres variables.
- Cuadro de correlación: se utiliza para mostrar la relación entre dos o más variables.
Aplicaciones de los cuadros matriciales
Los cuadros matriciales tienen una amplia variedad de aplicaciones en diferentes campos, incluyendo:
- Análisis de datos: se utilizan para visualizar y analizar grandes cantidades de datos.
- Toma de decisiones: se utilizan para presentar información clave para la toma de decisiones.
- Educación: se utilizan para presentar información de manera clara y concisa en el aula.
¿Qué es un gráfico matricial?
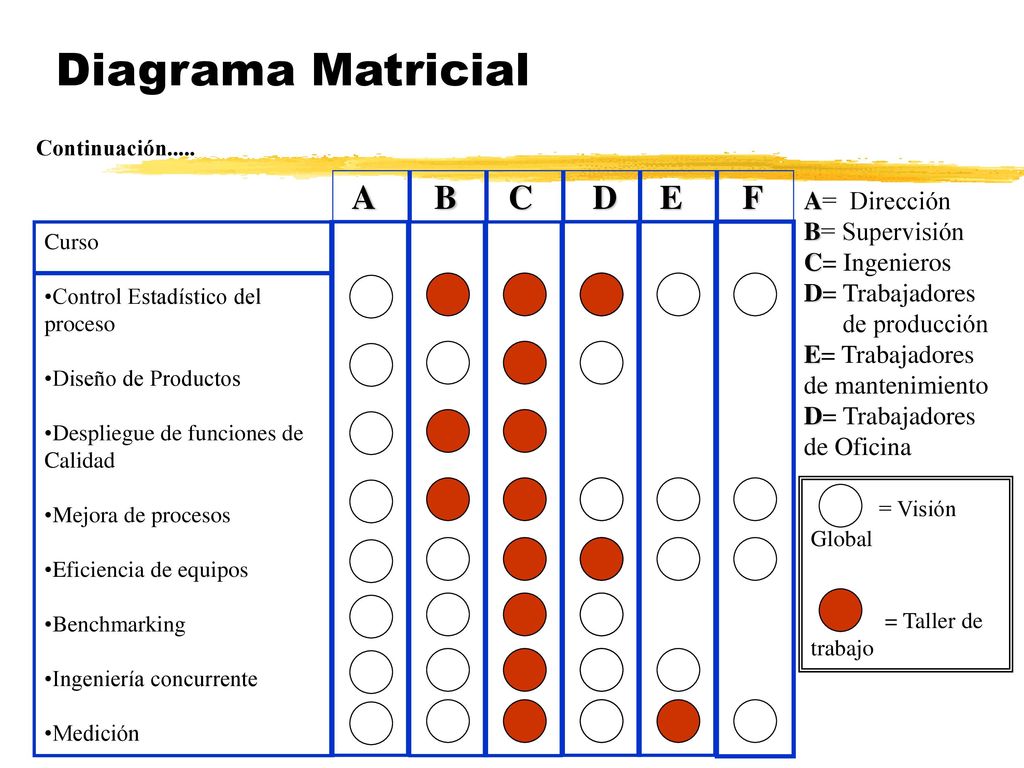
Un gráfico matricial es una representación gráfica utilizada en estadística y teoría de grafos para mostrar la relación entre diferentes variables o nodos en una matriz. Esta herramienta visual permite identificar patrones, relaciones y estructuras en los datos, lo que facilita la toma de decisiones y la comprensión de sistemas complejos.
Características de un gráfico matricial
Un gráfico matricial se caracteriza por tener los siguientes elementos:
- Matriz de adyacencia: es la representación de los nodos y sus conexiones en forma de una matriz.
- Nodos o vértices: son los elementos que se relacionan entre sí en el gráfico.
- Aristas o bordes: son las conexiones entre los nodos que indican la relación entre ellos.
Tipos de gráficos matriciales
Existen diferentes tipos de gráficos matriciales, cada uno con sus propias características y aplicaciones:
- Gráfico matricial de correlación: se utiliza para mostrar la relación entre variables continuas.
- Gráfico matricial de distancia: se utiliza para mostrar la distancia entre objetos o nodos.
- Gráfico matricial de similitud: se utiliza para mostrar la similitud entre objetos o nodos.
Aplicaciones de los gráficos matriciales
Los gráficos matriciales tienen una amplia gama de aplicaciones en diferentes campos, incluyendo:
- Análisis de redes sociales: para mostrar la relación entre individuos o grupos.
- Análisis de datos: para identificar patrones y relaciones entre variables.
- Visualización de datos: para mostrar la estructura y las relaciones en grandes conjuntos de datos.
Mas Informacion
¿Qué es un diagrama matricial?
Un diagrama matricial es una representación visual que utiliza una matriz para mostrar la relación entre diferentes elementos o variables. Estos diagramas se utilizan comúnmente en ingeniería, física, economía y otras disciplinas para analizar y visualizar la interconexión entre diferentes componentes o sistemas. En un diagrama matricial, las filas y columnas representan los diferentes elementos o variables, y cada celda de la matriz indica la relación entre los elementos correspondientes. Los diagramas matriciales pueden ser utilizados para identificar patrones, analizar la complejidad de un sistema y tomar decisiones informadas.
¿Cuál es el propósito de un diagrama matricial?
El propósito principal de un diagrama matricial es facilitar la comprensión y el análisis de la relación entre diferentes elementos o variables. Estos diagramas permiten identificar patrones y tendencias que no serían evidentes de otra manera, lo que puede ser útil en la toma de decisiones y la resolución de problemas. Los diagramas matriciales también pueden ser utilizados para comunicar información de manera efectiva a otros, ya que pueden ser más fáciles de entender que las tablas o las listas. Además, los diagramas matriciales pueden ser utilizados para identificar áreas de oportunidad para la mejora, optimizar procesos y reducir la complejidad de un sistema.
¿Cómo se crea un diagrama matricial?
Crear un diagrama matricial implica varios pasos. En primer lugar, es necesario identificar los elementos o variables que se van a analizar. Luego, se deben definir las filas y columnas de la matriz, lo que puede incluir la selección de los títulos de las filas y columnas. A continuación, se deben llenar las celdas de la matriz con la información relevante, lo que puede incluir números, símbolos o texto. Es importante asegurarse de que la información sea precisa y consistente. Finalmente, se puede personalizar el diagrama matricial añadiendo colores, imágenes o otras características para hacerlo más visualmente atractivo.
¿Cuáles son los beneficios de utilizar diagramas matriciales?
Los diagramas matriciales ofrecen varios beneficios. En primer lugar, permiten analizar y visualizar información compleja de manera efectiva. También facilitan la identificación de patrones y tendencias que no serían evidentes de otra manera. Los diagramas matriciales también pueden ser utilizados para comunicar información de manera efectiva a otros, lo que puede ser útil en la toma de decisiones y la resolución de problemas. Además, los diagramas matriciales pueden ayudar a identificar áreas de oportunidad para la mejora y optimizar procesos, lo que puede llevar a mejoras en la eficiencia y la productividad. Finalmente, los diagramas matriciales pueden ser utilizados para reducir la complejidad de un sistema, lo que puede llevar a una mayor claridad y comprensión.
Mira tambien: Revolutioniza tu Marketing con Banners Digitales
Revolutioniza tu Marketing con Banners Digitales Diseñador Gráfico: ¿Cuál es su Función?
Diseñador Gráfico: ¿Cuál es su Función? Triunfa como Growth Partner: Descubre los Secretos
Triunfa como Growth Partner: Descubre los Secretos Domina #Hashtags: Tu Guía 50 Caracteres al Éxito
Domina #Hashtags: Tu Guía 50 Caracteres al Éxito
Deja una respuesta